Boundary Value Problem Using Finite Difference Method

V list of ndarray. In this chapter we will start to introduce you the Fourier method that named after the French mathematician and physicist Joseph Fourier who used this type of method to study the heat transfer.

Finite Difference Method An Overview Sciencedirect Topics

A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions that are given on a hypersurface in the domain.

. Y y 0. The equation is defined on the interval 0 π 2 subject to the boundary conditions. Jac list of ndarray sparse matrix List of the Jacobian matrices of the constraints at the solution.

Here the linear basis functions have a value of 1 at their respective nodes and 0 at. The method uses a distance function to the true boundary to enforce Dirichlet boundary conditions on the non-aligned mesh faces therefore shifting the location where boundary conditions are imposed. In the field of numerical analysis meshfree methods are those that do not require connection between nodes of the simulation domain ie.

We saw this in the previous chapters that we can decompose a. The basic idea of this method is to express some complicated functions as the infinite sum of sine and cosine waves. To solve this equation in MATLAB you need to write a function that represents the equation as a system of first-order equations a function for the.

However since x_r is initially unknown there is no way to know if the initial guess is close enough to the root to get this behavior unless some special information about the function is known a priori eg the. Method equality_constrained_sqp tr_interior_point Optimization method used. Constr list of ndarray.

A Cauchy problem can be an initial value problem or a boundary value problem for. If x_0 is close to x_r then it can be proven that in general the Newton-Raphson method converges to x_r much faster than the bisection method. Here ψ i denotes the basis functions and u i denotes the coefficients of the functions that approximate u with u hThe figure below illustrates this principle for a 1D problem.

U could for instance represent the temperature along the length x of a rod that is nonuniformly heated. List of constraint values at the solution. Y 0 0.

The diffusion miniapp found in the miniappsshifted directory demonstrates the capability to formulate a boundary value problem using a surrogate computational domain. Total number of the conjugate gradient method iterations. For this example use the second-order equation.

Y π 2 2. Solve a second-order BVP in MATLAB using functions. A mesh but are rather based on interaction of each node with all its neighborsAs a consequence original extensive properties such as mass or kinetic energy are no longer assigned to mesh elements but rather to the single nodes.

Nous voudrions effectuer une description ici mais le site que vous consultez ne nous en laisse pas la possibilité.

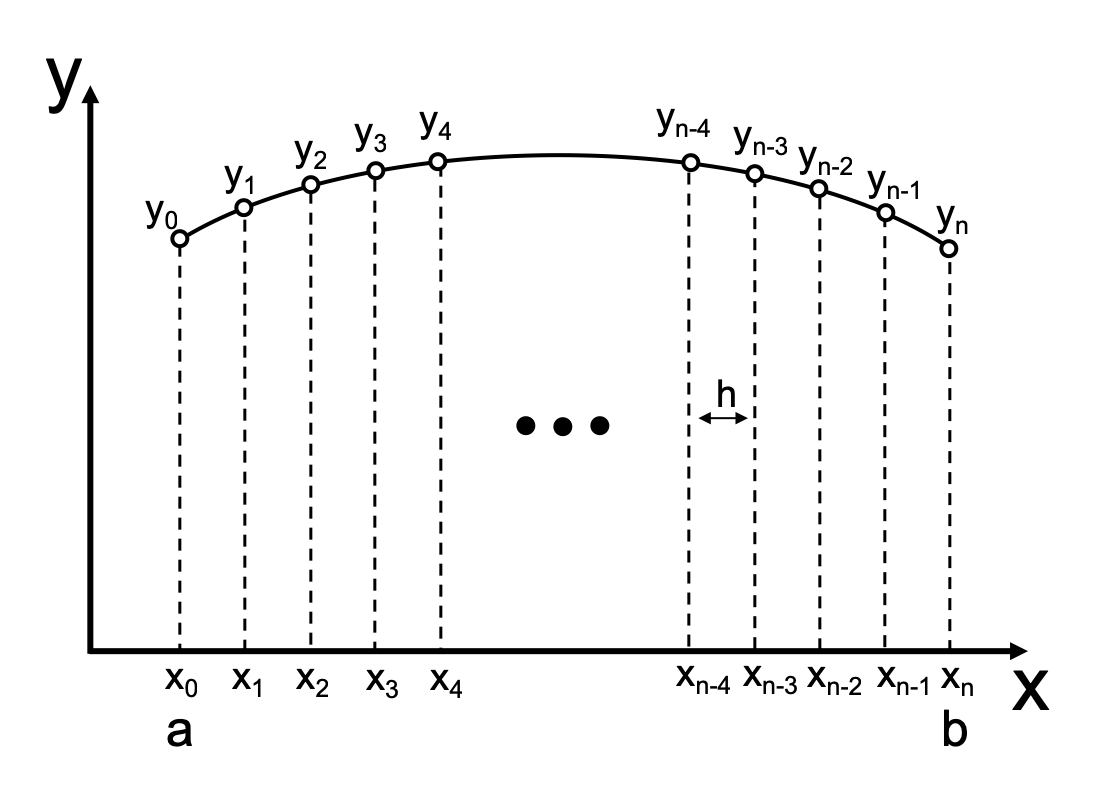
Finite Difference Method Python Numerical Methods

Heat Transfer L11 P3 Finite Difference Method Youtube

Finite Difference Method Python Numerical Methods

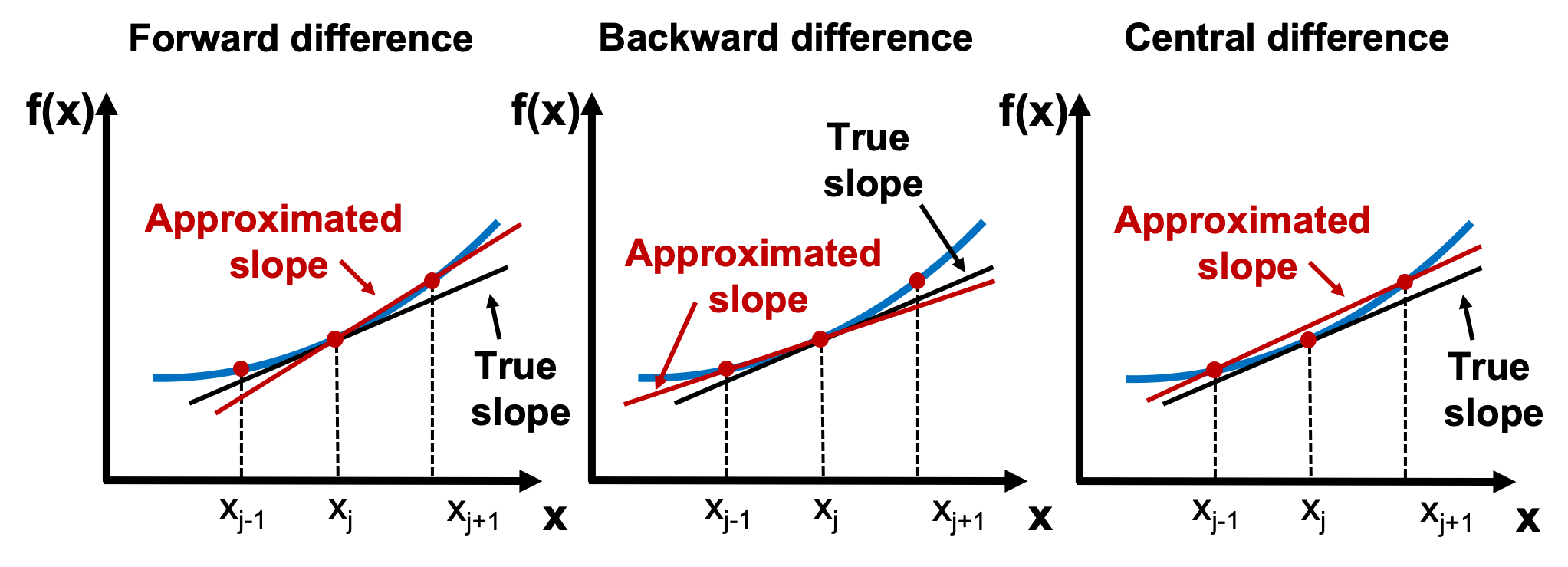
Finite Difference Approximating Derivatives Python Numerical Methods

Finite Difference Method Initial Value Problem Mathematics Stack Exchange

Approximating The Jacobian Finite Difference Method For Systems Of Nonlinear Equations Youtube